Summary: A juxtaposition of the work of economist Justin Wolfers and colleagues on the relationship between reported subjective well-being and income, and the Haushofer and Shapiro (2013) RCT estimates of well-being impacts for GiveDirectly.
Average well-being does seem to differ substantially by log income
In a previous post on the relationship between well-being and income, and the current distribution of income, I used a chart from Stevenson and Wolfers (2013) (by way of the Toby Ord and the Economist) to explore the case for log income (plus a constant) as a rough metric of human welfare.

[See here for some criticism of this research from Eric Falkenstein.] At economist Bryan Caplan's blog, Wolfers and Caplan had an exchange about the research with some interesting facts.
Caplan:
Wolfers replied to point out that such large disparities in income do exist across countries, over time, and considering the extremes of wealth within countries:

Reported experimental impacts of GiveDirectly on psychological well-being
Using Wolfers' equation, and assuming a wholly causal relationship, a doubling of income would correspond to an increase in average reported well-being of 0.35*ln(2)=0.24 standard deviations.
Haushofer and Shapiro (2013), an evaluation of the GiveDirectly transfers in Western Kenya 2011-2012 (which GiveWell "place[s] very high weight on", reports:
Average well-being does seem to differ substantially by log income
In a previous post on the relationship between well-being and income, and the current distribution of income, I used a chart from Stevenson and Wolfers (2013) (by way of the Toby Ord and the Economist) to explore the case for log income (plus a constant) as a rough metric of human welfare.
[See here for some criticism of this research from Eric Falkenstein.] At economist Bryan Caplan's blog, Wolfers and Caplan had an exchange about the research with some interesting facts.
Caplan:
Suppose you're a crude materialist who believes that money is the secret to happiness. You're estimating an equation of the form:
Happiness (in Standard Deviations) = a + b * ln(income)...
Last week Justin Wolfers came to GMU to present the best available individual, cross-national, and over-time evidence on income and happiness. After exploring a wide range of data sets, he gleefully presented the answer:
Happiness (in Standard Deviations) = a + .35 * ln(income)
Consider: Wolfers' result implies that to raise happiness by one standard deviation, you have to raise income by 1/.35=2.86 log points. How much is that exactly? In percentage terms, that's (e^2.86)-1 - an increase of 1,640%. So if you currently earn $50,000, Wolfers' coefficient implies you'd need an extra $820,585 per year to durably increase your happiness by one lousy standard deviation. In math, that's not "zero effect of income on happiness." But in English, it basically is.
Still not convinced? Remember that Wolfers deliberately refrains from controlling for confounding variables, so the true effect of income on happiness is almost certainly even smaller than it looks.
Wolfers replied to point out that such large disparities in income do exist across countries, over time, and considering the extremes of wealth within countries:
1. I'm not sure that controlling for confounds necessarily would reduce the causal effect of income. (My prior is similar to yours, but I haven't thought through the issue enough).
2. I actually think 0.35 is pretty big. Said another way, it's big enough that it can explain why people in Burundi are at 3.5/10 on a happiness scale, and Americans are at 8/10. My interpretation is that big gaps in happiness are easily explained by big gaps in income. So why do we interpret things differently?
a. I think raising happiness by a standard deviation is huge. Basically I see incredibly miserable people and incredibly happy people all around me. Moreover, if you think there's measurement error in happiness, then the standard deviation in measured happiness is even bigger (and you are talking about raising someone's measured happiness by one measured standard deviation).
b. The other way of saying this is that it doesn't matter that the effect of income on happiness is "small": if there exist massive disparatives in income, then a small coefficient can have a big effect. And I think there exist massive disparaties in income (and these largely explain the massive disparaties in happiness).
4. Your final thought experiment ("an extra $820,585" is clever). But it is just as interesting of a thought experiment in the opposite direction: If I raised your income from $3,000 (roughly the average income in the US at the turn of the century) to $50k, I would increase your happiness by one standard deviation. How many people would move from being "depressed" to OK? (If, for argument's sake, depressed = bottom 5% in 1900, then depressed = % of people with z-score less than 1.6. Shift that distribution 1 standard deviation to the right, and the proportion who are depressed = % of people with z-score+1 less than 1.6, which is 0.5%. So we would nearly eliminate depression.)Wolfers also pointed Caplan to this 2007 Gallup chart:
Reported experimental impacts of GiveDirectly on psychological well-being
Using Wolfers' equation, and assuming a wholly causal relationship, a doubling of income would correspond to an increase in average reported well-being of 0.35*ln(2)=0.24 standard deviations.
Haushofer and Shapiro (2013), an evaluation of the GiveDirectly transfers in Western Kenya 2011-2012 (which GiveWell "place[s] very high weight on", reports:
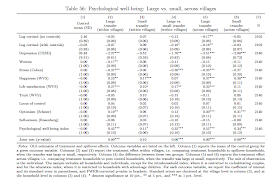
Transfers increase psychological well-being of recipients and their families. Unconditional cash transfers lead to a 0.18 SD increase in happiness, a 0.15 SD increase in life satisfaction, and a 0.14SD reduction in stress, all measured by psychological questionnaires. Large transfers lead to a reduction in levels of the stress hormone cortisol.Small transfers were $300, while large transfers were $1,100. The latter are around a year's household consumption, and had larger reported well-being effects. Results for large and small transfers within and between villages (although the confidence intervals don't cross 0 for the main well-being effects, they don't provide strong evidence for fine distinctions): [Table 56 from the appendix, HT Alex Berger:]
People who have earned $2X/year for a while might be less happy than people who earned $2X this year but used to earn $X/year until last year, because hedonic treadmill.
ReplyDeleteThe meaning of "one standard deviation" depends on what population you're looking at. In the GiveDirectly study, it appears to refer to one standard deviation in the distribution of happiness of the people in Western Kenya villages.
ReplyDeleteIt's not clear what population's standard deviation is being used in Wolfers' .35 estimate - perhaps the world's entire current adult population? One "world's standard deviation" is presumably larger than one "Western Kenya's standard deviation."
Dan, yes the SDs vary. Wolfers' statements and charts suggested this wasn't usually hugely important because of the large variation not accounted for by income, but certainly Kenya is further from the ceiling effects (you can't report a value above or below the given options).
ReplyDeleteI may try to get the data to check on this possibility.
Carl - thanks for the thoughtful post. I just want to note that the large and small transfer impacts aren't decomposable in the manner you're reporting. To get the figures you want, you need to look at Table 56 on page 82 of this PDF: http://web.mit.edu/joha/www/publications/Haushofer_Shapiro_UCT_Online_Appendix_2013.11.15.pdf
ReplyDeleteI don't think the results change too radically. But I would also guess that the study is underpowered to detected subtle differences in the slope of this variable.
Alexander, thanks, fixed. This post is written musing on a sanity check I was trying for the effect size, not anything to put much weight on.
ReplyDeleteWhat's your take on the Falkenstein / Easterlin hypothesis? The diagonal fit lines on those blobby graphs in Falkenstein's post sure did look spurious to me. Do you think his critique is valid?
ReplyDelete